解析概要
Advance/FrontFlow/redでキャビティ内に温度差を与え自然対流をシミュレートしました。 壁で密閉された空間において、壁面に温度差があると自然対流が発生します。 例えば、図1において左側壁面が右側壁面よりも高温で、上下壁面が断熱の場合には、 時計回りの自然対流が発生します。また、流動状態はグラフホフ数とプラント ル数の積であるレーリー数が小さい場合には層流状態で、レーリー数が大きくなるにつれて、 層流変動が生じて乱流に遷移することが知られています。
計算条件の概要
シミュレーションの計算条件は以下のように設定します。
1 計算領域
図1のような無次元距離 1×1 の正方形領域とし、 \(z\)軸負の向きに重力が加わります。
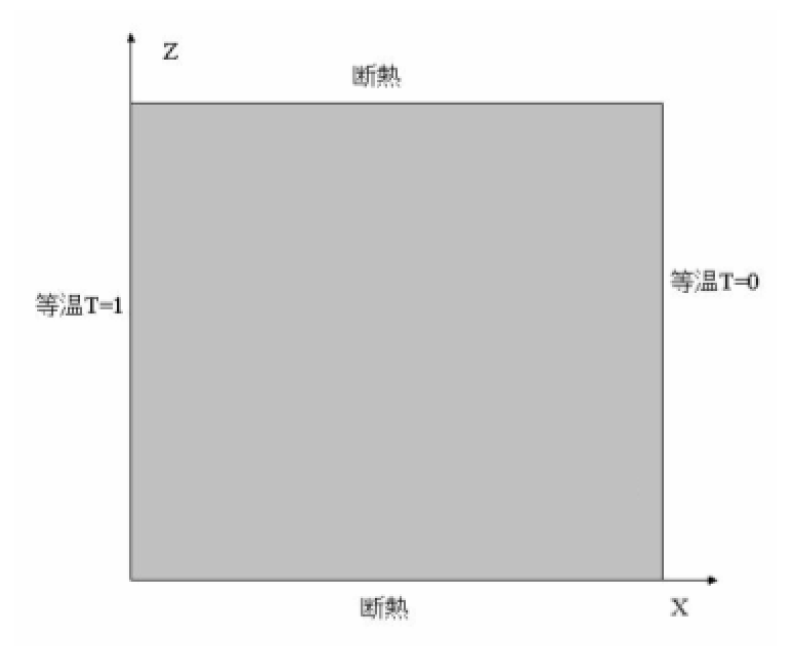
2 境界条件
| 境界 | 速度 | 温度 |
|---|---|---|
| 上下壁面 | 滑り無し | 断熱 |
| 左側 | 滑り無し | 1 |
| 右側 | 滑り無し | 0 |
3 物性値
| プラントル数 | レーリー数 |
|---|---|
| 0.71 | \(10^3\)と\(10^6\) |
解析結果
以下図2~4に計算結果の速度分布を示します。 左側の高温壁で温められ右側の低温壁で冷やされるため、密度は左から右に重くなり時計回りの対流が起こります。Ra\(=10^3\)からRa\(=10^6\)への間で層流から乱流への遷移があり、流れの特徴が変化しています。 高温壁における局所ヌッセルト数も図5のように傾向が変化します。
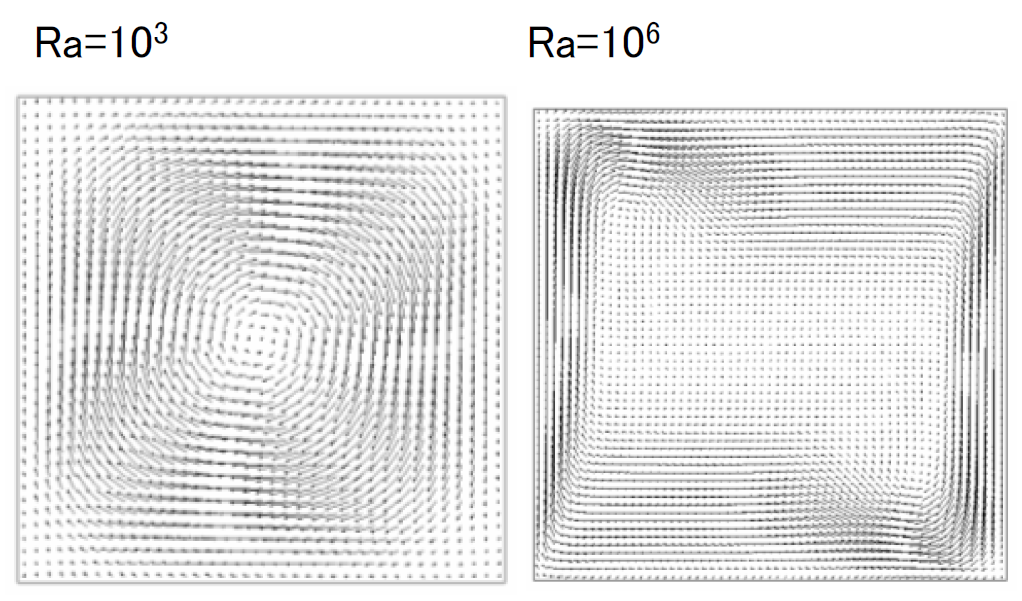
図2 速度ベクトル

図3 無次元速度分布。(a) 水平方向成分の等高線。(b)鉛直方向成分の等高線。
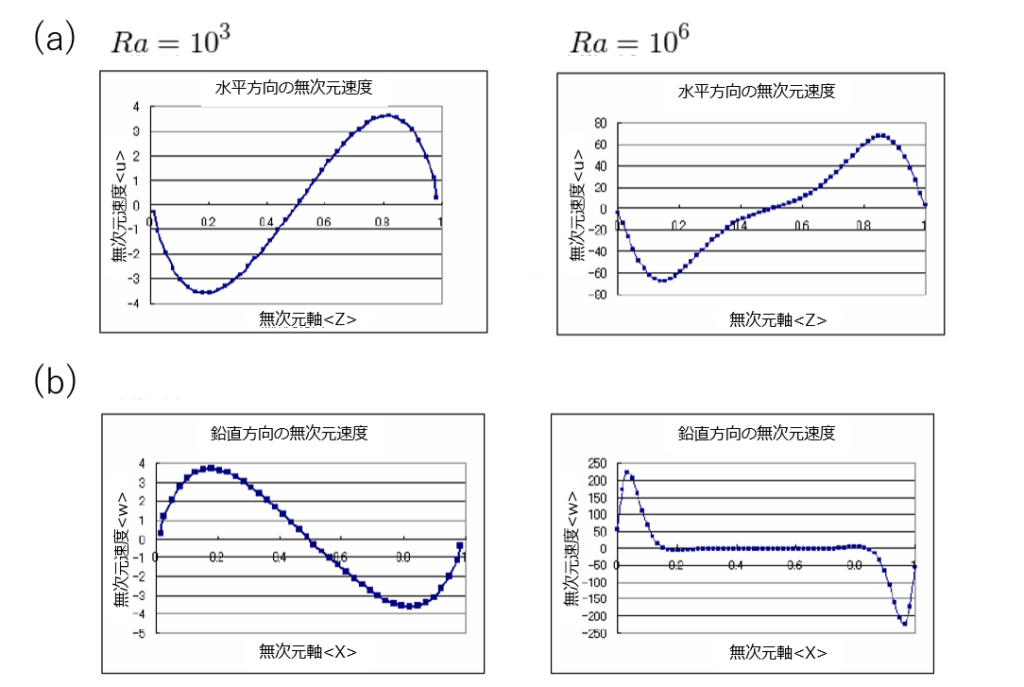
図4 断面速度分布。(a) 無次元速度水平方向成分の分布(x=0.5)。(b)無次元速度鉛直方向成分の分布(z=0.5)。
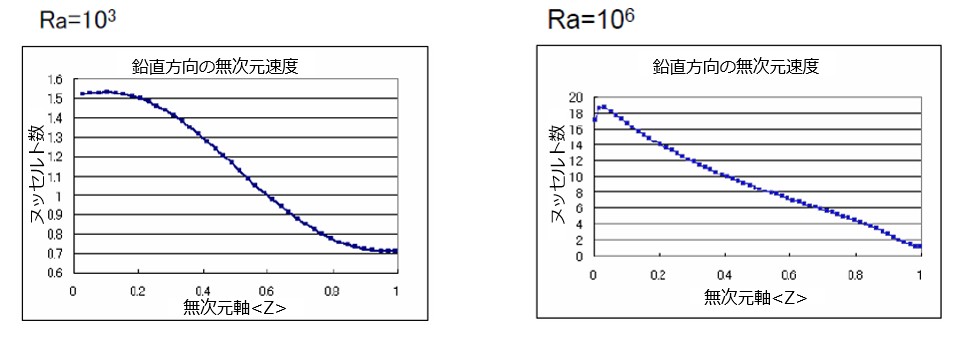
図5 高温壁における局所ヌッセルト数。
最後に本解析と文献値の比較を表1に示します。
| Ra\(=10^3\) | 文献[1] | Ra\(=10^6\) | 文献[1] | ||
|---|---|---|---|---|---|
| 水平方向速度 の最大値 | \(U_\rm{max}\) | 3.641 | 3.649 | 67.68 | 64.63 |
| と 位置\((X=0.5)\) | \(Z_\rm{max}\) | 0.8205 | 0.813 | 0.8644 | 0.850 |
| 鉛直方向速度 の最大値 | \(W_\rm{max}\) | 3.693 | 3.697 | 222.17 | 219.36 |
| と 位置\((Z=0.5)\) | \(X_\rm{max}\) | 0.1794 | 0.178 | 0.0338 | 0.0379 |
| 最大ヌッセルト数 | \({Nu}_\rm{max}\) | 1.531 | 1.505 | 18.733 | 17.925 |
| と高温壁における 位置 | \(Z_\rm{max}\) | 0.1025 | 0.092 | 0.0339 | 0.0378 |
| 最小ヌッセルト数 | \({Nu}_\rm{min}\) | 0.711 | 0.692 | 1.214 | 0.989 |
| と高温壁における 位置 | \(Z_\rm{min}\) | 1.0 | 1.0 | 0.983 | 1.0 |
| 高温壁の平均ヌッセルト数 | 1.1372 | 1.118 | 9.14 | 8.8 |
適用例
- 自然対流・強制対流の関わる現象
- 冷暖房、熱交換機など
参考文献
[1] De Vahl Davis,G, Natural convection of air in a square cavity: A bench mark numerical solution, Int. J. Numer. Meth. Fl. 3 (1983), 0271-2091

