概要
逆火(フラッシュバック、flashback)とは、 火炎速度(または火炎の進行速度)が流体の流速を上回ったときに、火炎が流れに逆行して上流へ進行する現象です。 燃焼している火炎が流れに逆らって上流方向(バーナー内部やノズル内部)に侵入してしまうため、特に予混合燃焼で安全上の重要な問題となります。 逆火の発生メカニズムには、3つあり、1つは火炎の速度と流速の関係です。 流速\(u\)が火炎の層流燃焼速度\(S_L\)より小さいと、火炎は上流に向かって進行可能となります。 つまり、逆火は次の条件で起こります。
\[u<S_L\]
特に、バーナー壁面や境界層付近では流速がゼロ近くになるため、逆火が起こりやすくなります。 次に、乱流の影響があります。 予混合燃焼では、火炎が乱流の中で波打つため、火炎の表面積が増大し、実効燃焼速度が上がります。 つまり、逆火しやすくなります。 3つ目が再循環領域の存在です。 Bluff-bodyやスワールジェットがあると、再循環領域が形成され、そこに火炎が補足され、そこから上流へ進むこともあります。
本項では、当社の CFD ソフト Advance/FrontFlow/redを用いて、 メカニズムの1つ目である火炎の速度と流速の関係を調査するために、 2次元層流予混合燃焼解析を行い、先行研究のある逆火限界の予測結果(Fruzza et al. 2024)と比較しました。
解析条件
表1が解析条件となります。 化学反応メカニズムには、Smithらにより提案され、広く使用されているGRI-Mech3.0 (Smith et al. 2003)と、 Bilgerらにより提案されたCH4燃焼用のreduced mechanism (Bilger et al. 1990)を使用し、両者の予測精度を比較しました。 ここで、GRI-Mech3.0は、53化学種325反応を用いた、NOxの形成、再着火を含む、天然ガスの燃焼用に最適化された化学反応メカニズムです。対して、reduced mechanismは同じくメタン燃焼に対応した化学反応メカニズムですが、 17化学種58反応と比較的計算負荷の軽いメカニズムとなっています。
表1:解析条件
| 項目 | 設定 |
| ソルバ | Advance/FrontFlow/red ver.5.8 |
| 支配方程式 | 圧縮性 Navier-Stokes 方程式 |
| 空間離散化 | 有限体積法+セル中心法 |
| 対流項スキーム | 運動量、エネルギー、化学種ともに2次精度風上差分法 |
| 圧力ー速度カップル法 | SIMPLE法 |
| 勾配計算 | Green Gauss法 |
| 時間積分 | Euler陰解法 |
| 行列計算 | ICCG法 |
| 乱流モデル | なし (層流流れ) |
| 化学反応 | 素反応モデル(逆反応の係数は化学平衡の概念から算出) |
| 化学反応機構 | GRI-Mech3.0 (Smith \(et \,al.\) 2003)、Reduced mechanism (Bilger \(et \,al.\) 1990) |
| 熱力学変数 | NASA7多項式によるモデル化 |
| 輸送係数 | 粘性、拡散係数、熱伝導率ともにLennard-Jonesパラメータを用いた実在物性 |
図1に解析領域の概要と、表2に各設定変数説明を示します。 本解析では、2次元のシンプルな計算格子を使用します。 セル数は約2.1万セルとなりました(約4.5万点)。 流入境界から CH4-H2-Air の予混合ガスが流れてきて、 スリット部により流れが加速されるため、その位置で保炎します。 この状態で、流入速度 \(V_{in}[m/s]\) を徐々に下げていきます。 スリット位置での流速 \(V_{s}[m/s]\) がある流速 \(V_S |_{FB} [m/s]\) よりも小さくなると、流速よりも火炎の伝播速度が大きくなり、保炎されていた火炎がスリット上流へ伝播します。 この流速 \(V_S |_{FB} [m/s]\) が、逆火限界の速度となります。 本解析では、時間発展項を緩和項として定常解を求める方法を用いており、 時間刻みを \(\Delta t=1.0×10^{−6}[s]\) として、流入速度を変更しながら定常解を取得しました。 使用したCPU数は、56 CPUsとなっています。
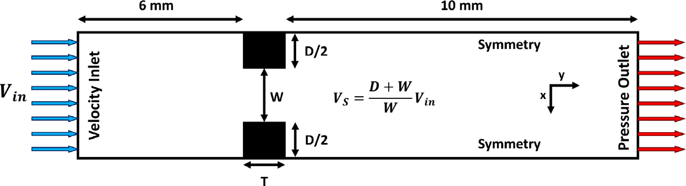
図1:計算領域 (Fruzza \(et \,al.\) 2024)
表2:変数の説明と値の設定
| 変数 | 意味 | 値 |
| \(W\) | スリット幅 | \(1[mm]\) |
| \(D\) | 隣り合うスリット間の幅 | \(\displaystyle \frac{W}{D} = 0.5\) |
| \(T\) | バーナー厚さ | \(0.6[mm]\) |
| \(V_{in}\) | 流入速度 | 逆火の起こらない条件から徐々に減少させる |
| \(V_{s}\) | スリット位置での流れの速度 | \(\displaystyle \frac{D+W}{W} V_{in} [m/s]\) |
| \(T_{u}\) | 流入温度 | \(300[K]\) |
| \(P_{exit}\) | 出口圧力 | \(1[atm]\) |
| \(p_{s}\) | 固体密度 (stainless steel) | \(7719[kg/m^3]\) |
| \(c_{p,s}\) | 固体比熱 (stainless steel) | \(461.3[J/(kg⋅K)]\) |
| \(k_{s}\) | 固体熱伝導率 (stainless steel) | \(22.54[W/(m⋅K)]\) |
| \(V_{FB}\) | 逆火限界速度 | \(V_{S} |{FB} = \displaystyle \frac{D+W}{W} V{in} |_{FB} [m/s]\) |
参考論文(Fruzza et al. 2024)では、 予混合ガスの組成の他に、スリット部のサイズ \(W\)、\(D\) を変更した様々な解析を行っていますが、 今回の解析では予混合ガスの組成に着目して、スリットのサイズを統一した、図2、表3に示す7ケースを行います。
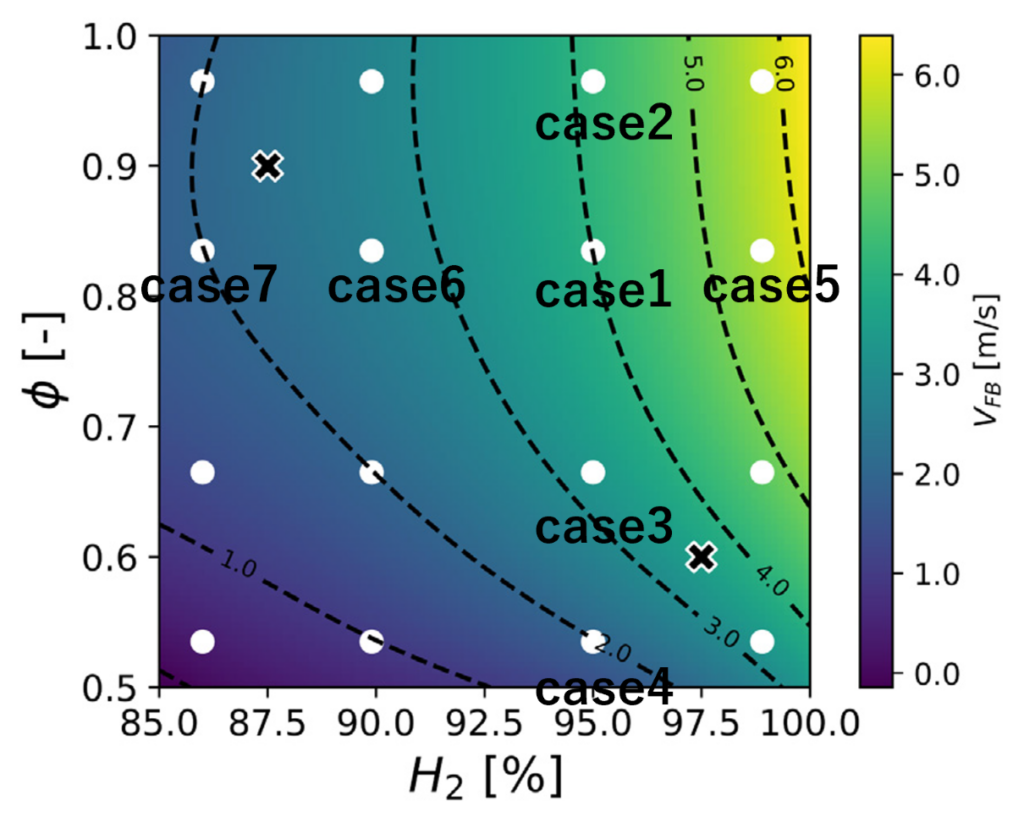
図2:先行研究における各ケースの条件と逆火限界速度 (Fruzza \(et \,al.\) 2024)
表3:各ケースの質量分率組成と逆火限界速度
| Case | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| \(\%H2\) | 95% | 95% | 95% | 95% | 98.9% | 89.9% | 86% |
| \(\phi\) | 0.835 | 0.965 | 0.665 | 0.535 | 0.835 | 0.835 | 0.835 |
| \(Y_{H2}\) | 0.0197 | 0.0226 | 0.0157 | 0.0127 | 0.0229 | 0.0164 | 0.01435 |
| \(Y_{CH4}\) | 0.0082 | 0.0095 | 0.0066 | 0.0053 | 0.0020 | 0.0146 | 0.01860 |
| \(Y_{O2}\) | 0.2266 | 0.2257 | 0.2269 | 0.2289 | 0.2273 | 0.2258 | 0.2253 |
| \(Y_{N2}\) | 0.7455 | 0.7419 | 0.7508 | 0.7530 | 0.7478 | 0.7432 | 0.7417 |
| \(V_{FB} [m/s]\) | 4.0 | 4.2 | 3.4 | 2.0 | 5.7 | 2.7 | 2.0 |
解析結果
動画1、2では、Advance/FrontFlow/red での解析により得られた解析結果の温度分布、OH質量分率分布を示しており、2つの化学反応メカニズムで比較しています。 ここでは、特徴的な2つのケースの結果を示しています。 まず、case2(動画1)は比較的高い\(\%H2\) と \(\phi\)となっており、逆火限界速度も比較的高いものとなっています。 このケースでは、2つの化学反応メカニズムの違いはそれほど見られませんでした。 続いて、case4動画2では、\(\%H2\) は高いのに対して、\(\phi\) は低めで、逆火限界速度も低いものとなっています。 このケースでは、2つの化学反応メカニズムの違いが顕著に見られ、 GRI-Mech3.0(Smith et al. 2003)の方が燃焼速度が低く予測されるということが分かりました。
動画1:Case2における逆火限界予測の結果。動画において、左から温度分布(簡略化反応機構)、温度分布(GRI-Mech3.0)、OH の質量分率分布(簡略化反応機構)、OH の質量分率分布(GRI-Mech3.0)を表しています。
動画2:Case4における逆火限界予測の結果。動画において、左から温度分布(簡略化反応機構)、温度分布(GRI-Mech3.0)、OH の質量分率分布(簡略化反応機構)、OH の質量分率分布(GRI-Mech3.0)を表しています。
最後に表4にて、2つの化学反応メカニズムを使って Advance/FrontFlow/red により予測された、逆火限界速度を先行研究 (Fruzza et al. 2024)と比較します。 全体として、予測された逆火限界速度は先行研究の結果とよく一致しました。 Case1,5が最も誤差が小さく、対して、case4が最も誤差が大きいものとなりました。 前述した通り、case4は \(\%H2\) の割合が多く、\(\phi\) が低い組成となっており、 特にGRI-Mech3.0では、そのような条件での燃焼速度の予測精度はあまり高く無いと考えられます。 対して、同じ逆火限界速度であるcase7は比較的誤差が小さい結果となりました。 こちらは \(\%H2\) の割合がそれほど高くなく、化学反応メカニズムが対象としている炭化水素系の CH4中心の燃焼速度の予測精度は高いことがわかります。
表4:予測された逆火限界速度と先行研究との差異
| Case | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| \(V_{FB}[m/s]\) (Fruzza et al., 2024) | 4.0 | 4.2 | 3.4 | 2.0 | 5.7 | 2.7 | 2.0 |
| \(V_{FB}[m/s]\) (AFFr with reduced mechanism) | 4.02(+0.5%) | 4.23(+0.7%) | 3.36(+1.2%) | 1.86(−7.0%) | 5.73(+0.5%) | 2.71(+0.4%) | 2.00(+0.0%) |
| \(V_{FB}[m/s]\) (AFFr with GRI-Mech3.0) | 4.00(+0.0%) | 4.22(+0.5%) | 3.24(−4.7%) | 1.53(+23.5%) | 5.70(+0.0%) | 2.68(−0.7%) | 1.97(−1.5%) |
層流火炎の逆火現象を詳細化学反応機構により再現しました。 本項の結果から、 GRI-Mech3.0 (Smith et al. 2003)のような複雑な反応メカニズムが万能な反応メカニズムとは限らないことがわかりました。 逆火限界の再現には、燃料に応じた燃焼速度を適切に再現できる反応メカニズムを選択することが重要です。 Advance/FrontFlow/red ではユーザーにより化学反応機構を任意に設定することが可能であるため、計算コストや計算精度を考慮した解析が可能です。 どれを使えばよいか分からないユーザーへは、複数のモデルの中から適切なモデルを提供可能です。 Advance/FrontFlow/red を用いることで、炉内におけるガスの燃焼やそれによる固体への熱伝達、 さらには、逆火などの安全性に関わる現象を事前に予測することが可能となります。
参考文献
- Fruzza, F., Lamioni, R., Mariotti, A., Salvetti, V. M., Galletti, C., “Flashback propensity due to hydrogen blending in natural gas: Sensitivity to operating and geometrical parameters,” Fuel, Vol. 362, 130838, 2024.
- Smith, P. G., Golden, M. D., Frenklach, M., Moriarty, W. N., Eiteneer, B., Goldenberg, M., Bowman, T. C., Hanson, K. R., Song, S., Gardiner, C. W. Jr., Lissianski, V. V., & Qin, Z., “GRI-Mech 3.0,” http://www.me.berkeley.edu/gri_mech/, 2003 (Accessed May, 2025).
- Bilger, R., Starner, S., Kee, R., “On reduced mechanisms for methane-air combustion in non-premized flames,” Combustion and Flame, Vol. 80, Issue 2, pp. 135-149, 1990.

