概要
保炎のために、bluff bodyを保炎機構としたバーナーを設計する場合があります(TNF Workshop)。 Bluff bodyによりジェット出口付近に再循環流れが発生し、これにより火炎が保持されます。
本項では、当社の CFD ソフト Advance/FrontFlow/red 搭載の、詳細化学反応機構の検証問題として、 CH4/H2 bluff body burnerの定常Reynolds-Averaged Navier-Stokes(RANS)解析を行い、 先行研究(Ren et al. 2013)の結果との比較を行いました。
解析条件
表1 が解析条件となります。 化学反応メカニズムには、Smithらにより提案され、広く使用されているGRI-Mech3.0(Smith et al. 2003)を使用しました。 GRI-Mech3.0は、NOxの形成、再着火を含む、天然ガスの燃焼用に最適化された化学反応メカニズムです。 また、先行研究の解析は乱流燃焼モデルの1つであるEddy dissipation concept (EDC) (Magnussen 1981)を使用しており、 Advance/FrontFlow/red の解析においてEDCを用いた解析、用いない解析を行い、両者の解析結果を比較します。
表1:解析条件
| 項目 | 設定 |
| ソルバ | Advance/FrontFlow/red ver.5.8 |
| 支配方程式 | 低マッハ数近似 Reynolds-Averaged Navier-Stokes (RANS)方程式 |
| 空間離散化 | 有限体積法+セル中心法 |
| 対流項スキーム | 運動量、エネルギー、化学種、乱流モデル変数ともに2次精度風上差分法 |
| 圧力ー速度カップル法 | SIMPLE法 |
| 勾配計算 | Green Gauss法 |
| 時間積分 | Euler陰解法 |
| 行列計算 | ICCG法 |
| 乱流モデル | Standard \(k-\epsilon\)乱流モデル |
| 化学反応 | 素反応モデル(逆反応の係数は化学平衡の概念から算出) |
| 化学反応機構 | GRI-Mech3.0 (Smith \(et \,al\). 2003) |
| 乱流燃焼モデル | なし/Eddy dissipation concept (Magnussen 1981) |
| 熱力学変数 | NASA7多項式によるモデル化 |
| 輸送係数 | 粘性、拡散係数、熱伝導率ともにLennard-Jonesパラメータを用いた実在物性 |
解析格子の概要を図1、2に示します。本解析では、2次元で作成した計算格子を5deg分(1セル分)回転押し出しをして、 2.5次元の格子を作成しました。セル数はmedium格子で約1.1万セル、fine格子で約3.3万セルとなりました。 図3、4は流入面の拡大図を示しており、 ジェット部の直径は\(D_j=3.6\)[mm]、bluff bodyも含めた直径は\(D_b=50\)[mm]となっています。
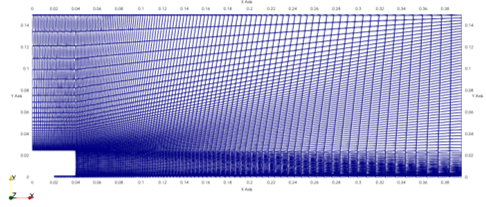
図1:Medium格子断面図
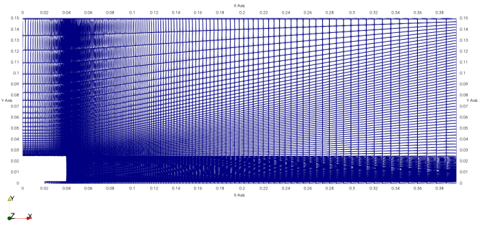
図2:Fine格子断面図
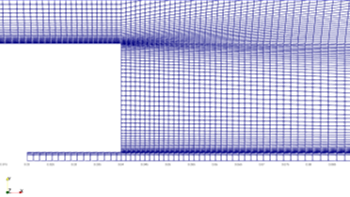
図3:Bluff body拡大図(Medium格子)
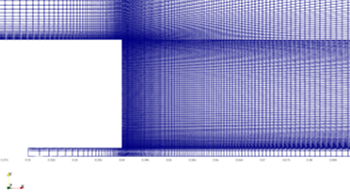
図4:Bluff body拡大図(Fine格子)
今回の解析では体積比で \(V_(CH4):V_(H2)=1:1\) による燃料ジェットを中心部から噴出し、 周りから空気が低速で流入します。初期条件において、温源として高温領域を設定し火炎の発達を促します。 時間発展項を緩和項として定常解を求める方法を用いており、 流れ場の素早い発達のために時間刻みを\(\Delta t=5.0×10^{−6}[s]\)としました。 使用したCPU数は、56 CPUsとなっています。
解析結果
以下では、Advance/FrontFlow/red での解析により得られた速度の大きさ\(\overline{U}[m/s]\) 分布(図5)、 定常解の温度 \(\overline{T}[K]\) 分布(図6)、 OH質量分率 \(\overline{Y_{OH}}\) 分布(図7)を示しており、 図6、7については先行研究(Ren et al. 2013)と比較しています。 ここでは、 比較的大きなbluff bodyによりジェット出口に低速の再循環流れが発生していることが分かります(図5)。 そして、再循環流の外縁から火が付き、同時に中間生成物としてOHが生成されていることが確認できます(図6、7)。 Bluff bodyがあることにより、Sandia H2 flame (Barlow et al. 2003)と比較して、火炎の形態が大きく異なることが分かります。 格子を細分化することにより、ジェット流の減衰が小さくなり、火炎がより下流まで広がっている様子が見られます。 また、bluff body付近の流れも変化することにより、温度分布や生成物の分布も変化しています。 今回のジェット条件では、EDC導入の効果は小さく、下流にてやや拡散が大きくなる程度でした(図7)。
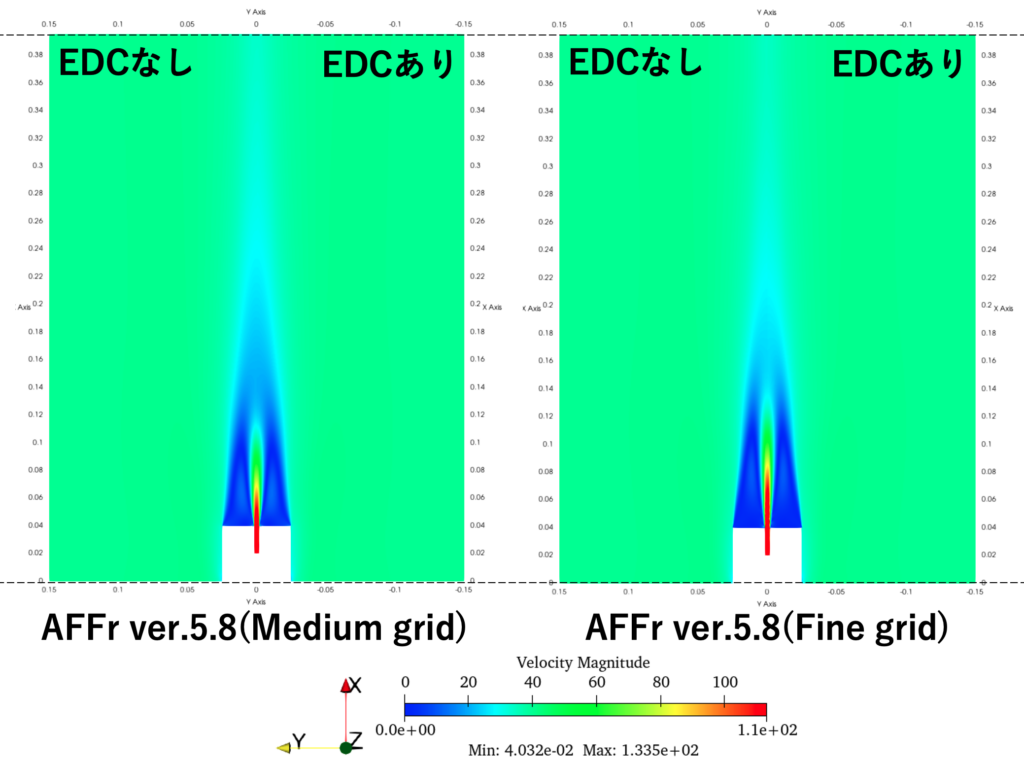
図5:速度の大きさ\(\overline{U} = \overline{\sqrt{\overline{u}^2 + \overline{v}^2 + \overline{w}^2}} [m/s]\)分布
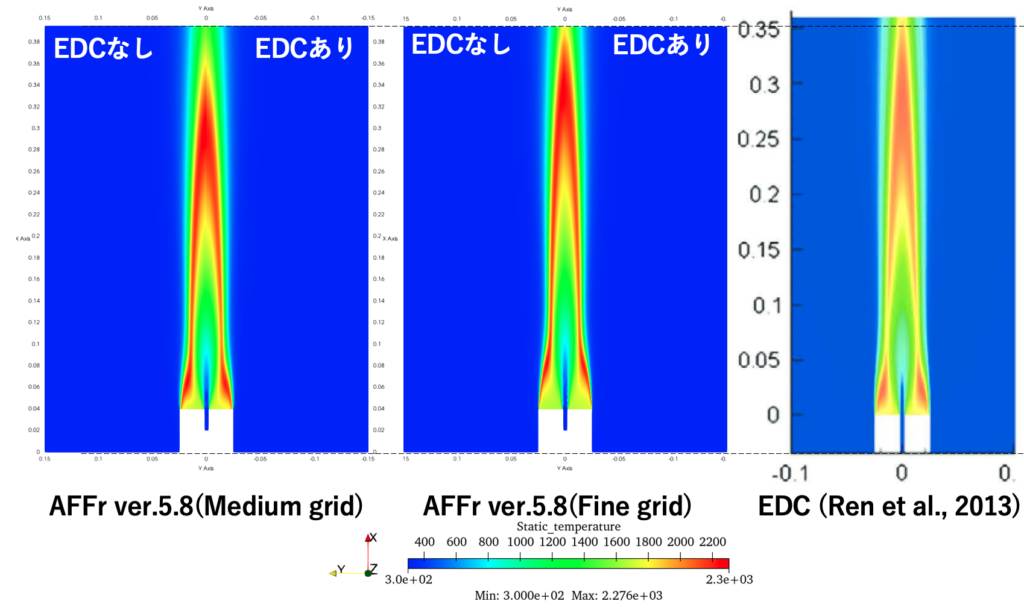
図6:温度 \(\overline{T}[K]\)分布
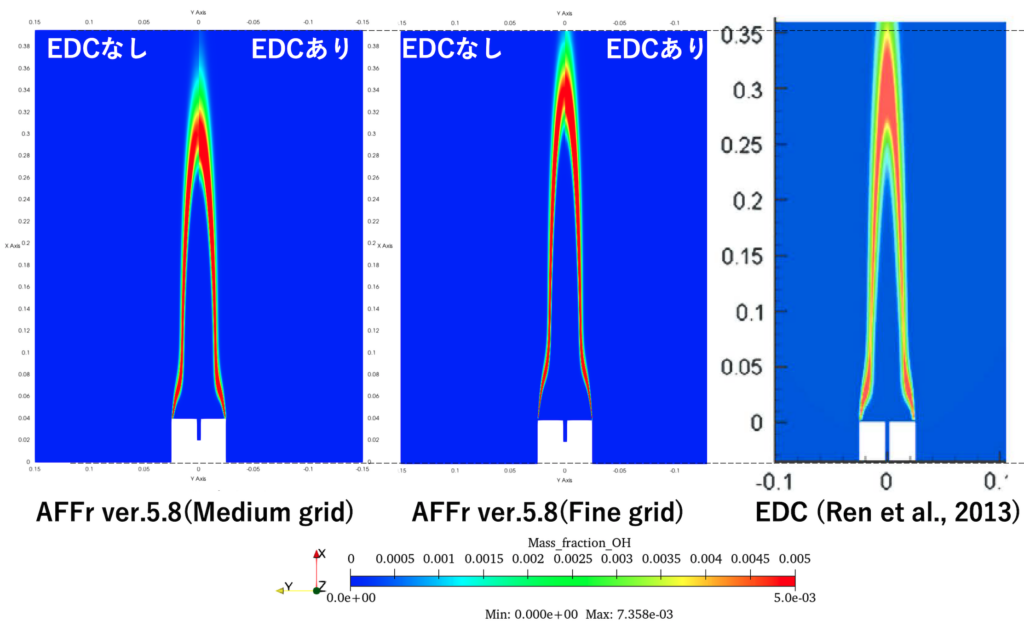
図7:OH質量分率 \(\overline{Y_{OH}}\)分布
次に、図8〜15に、各流れ方向位置 \(x/D_b\) における、平均温度\(\overline{T}[K]\)と平均OH質量分率 \(\overline{Y_{OH}}\) の半径方向分布を実験値と先行研究(Ren et al. 2013)とともに比較します。 Medium格子の結果は、先行研究(Ren et al. 2013)の解析結果と比較的よく一致しており、 更に格子を細かくしたFine格子では再循環流付近の温度分布や \(\overline{Y_{OH}}\)のピーク位置が実験値に近づいていることが確認できます。 これは、格子が細かくなったことで再循環流が変化したためと考えられます。 定量的な比較においてもEDCの影響はあまり見られない結果となりました。
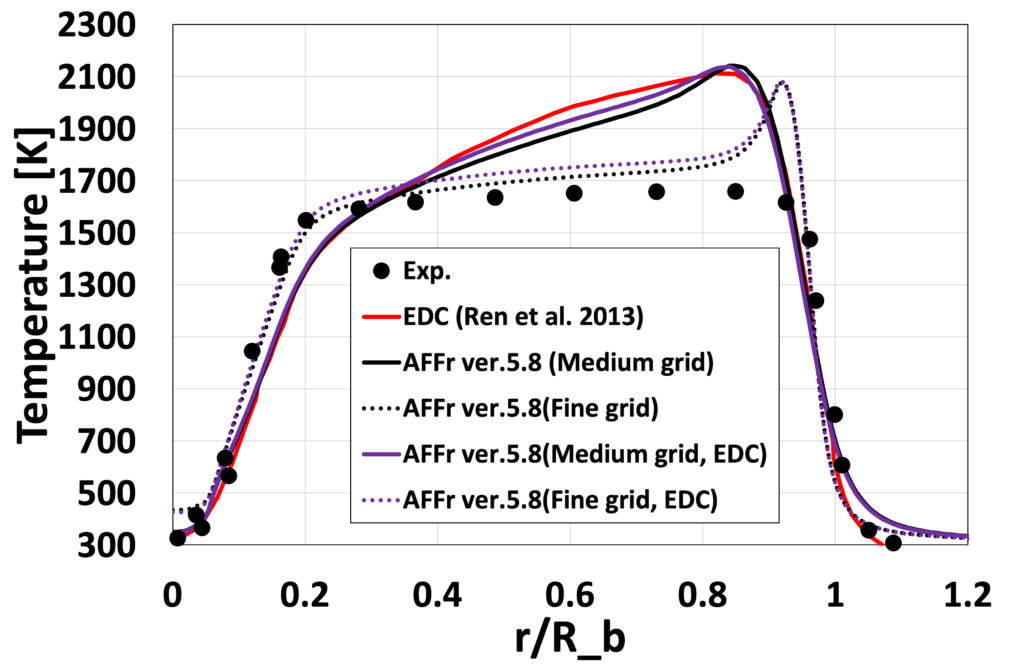
図8:半径方向温度 \(\overline{T}[K]\)分布 (\(x/D_b=0.26\))

図9:半径方向温度 \(\overline{T}[K]\)分布 (\(x/D_b=0.6\))
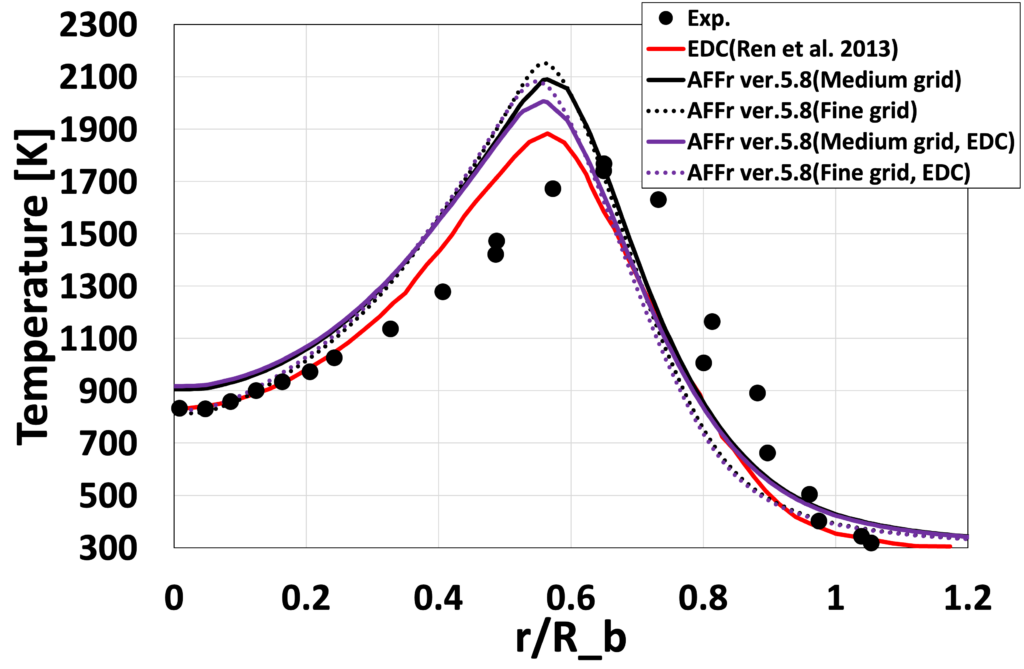
図10:半径方向温度 \(\overline{T}[K]\)分布 (\(x/D_b=1.3\))
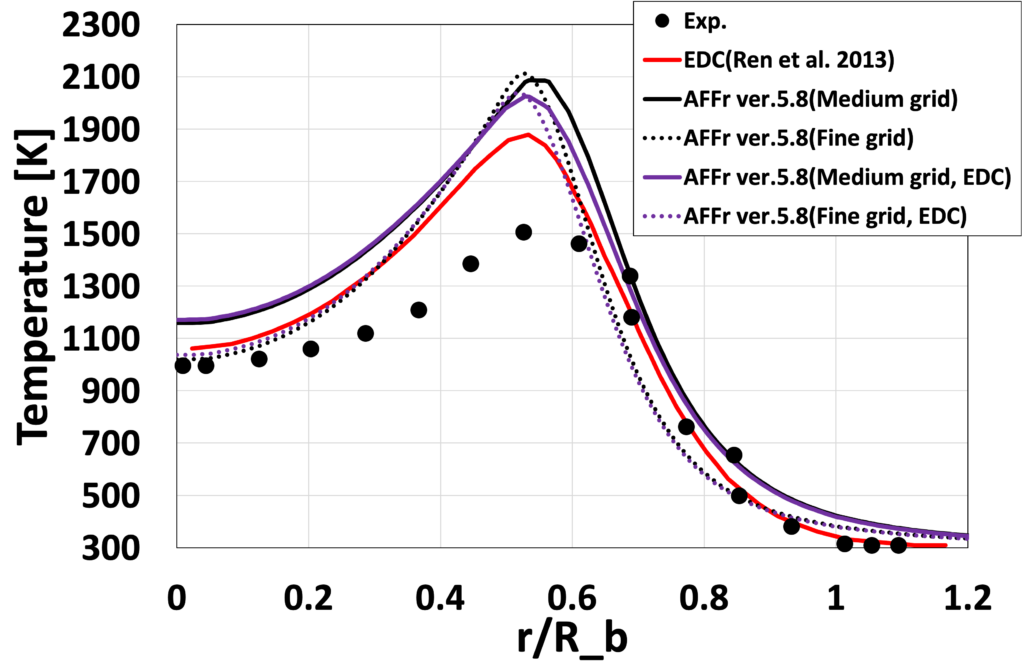
図11:半径方向温度 \(\overline{T}[K]\)分布 (\(x/D_b=1.8\))
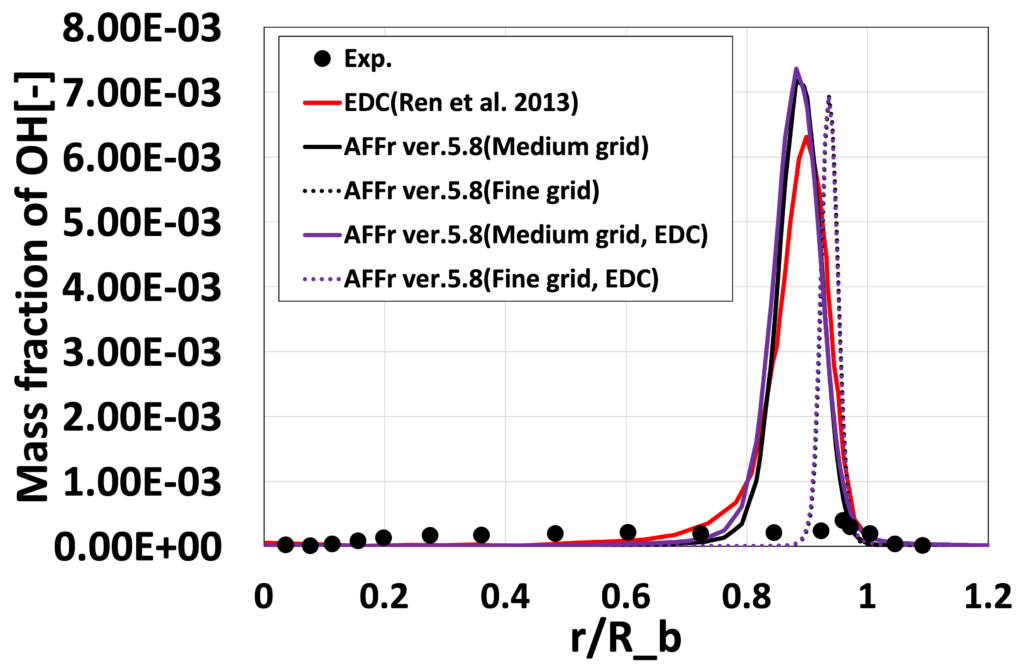
図12:半径方向OH質量分率 \(\overline{Y_{OH}}\)分布 (\(x/D_b=0.26\))
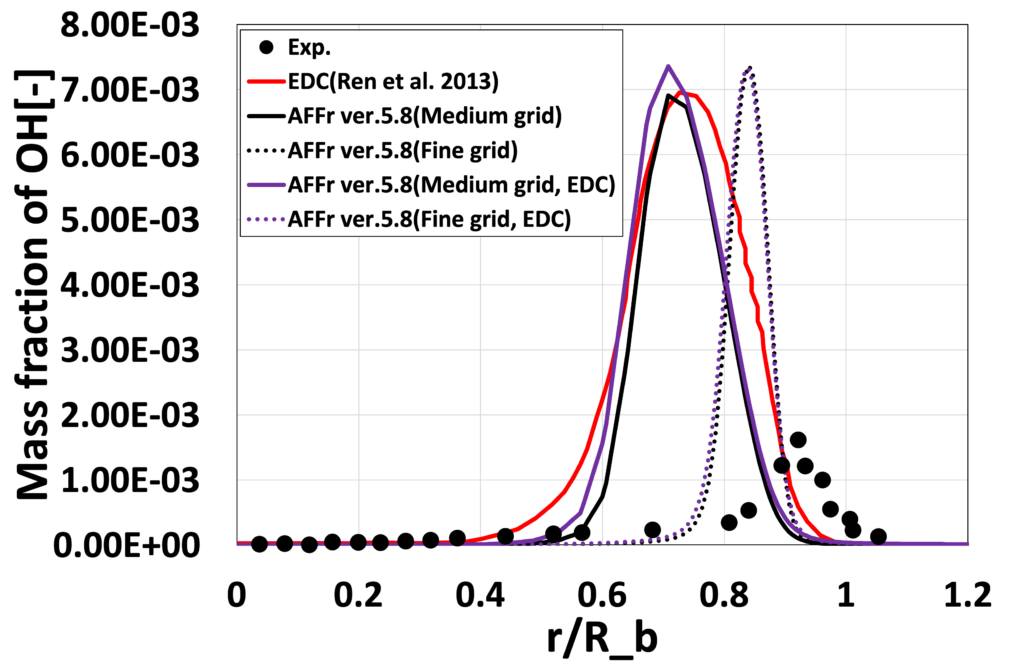
図13:半径方向OH質量分率 \(\overline{Y_{OH}}\)分布 (\(x/D_b=0.6\))
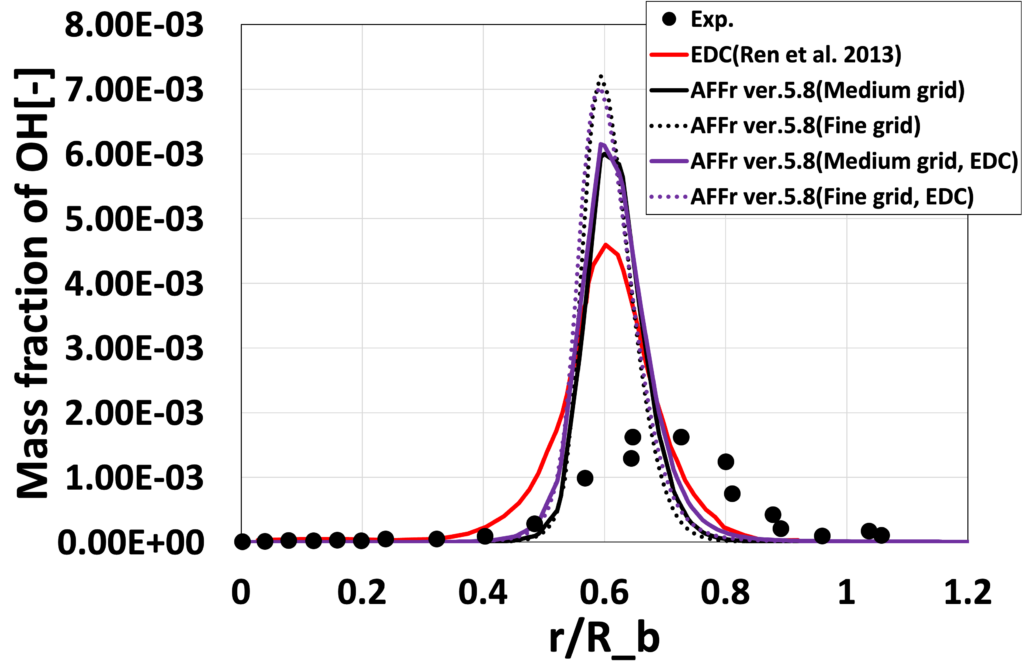
図14:半径方向OH質量分率 \(\overline{Y_{OH}}\)分布 (\(x/D_b=1.3\))
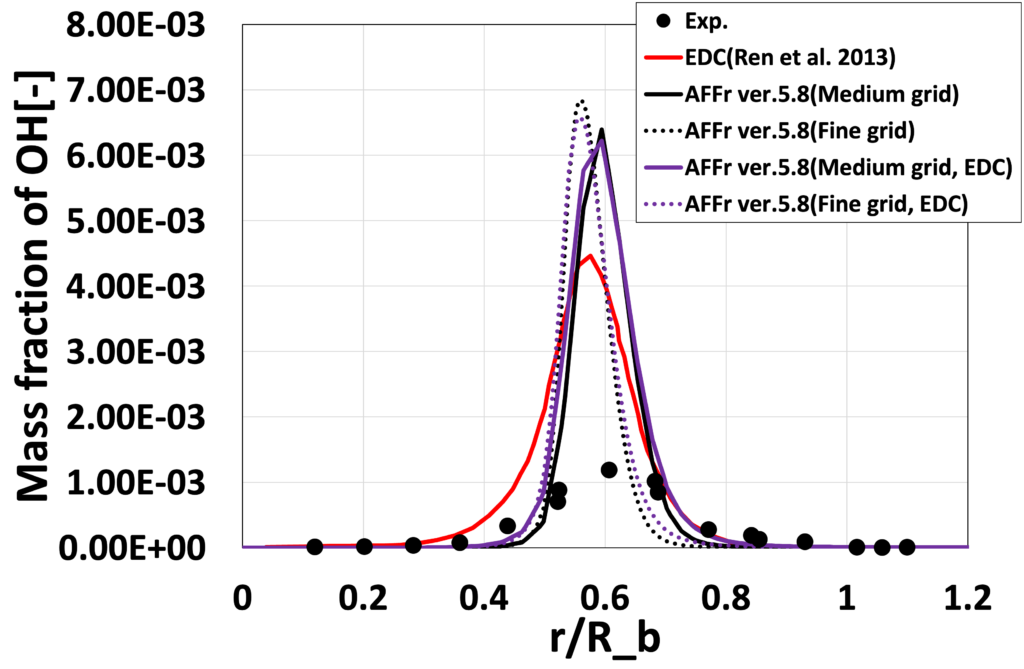
図15:半径方向OH質量分率 \(\overline{Y_{OH}}\)分布 (\(x/D_b=1.8\))
最後に、図16〜19にEDCモデルを使用しないMedium格子による解析結果の、各位置での主要な化学種の質量分率\(\overline{Y_i}\)分布、 図20〜23に主要な化学反応の反応速度 \(\overline{\dot{\omega}_j} [mol/ \left( m^3 \cdot s \right)]\)の分布を示します。 表2には、GRI-Mech3.0中における、OHの生成に関わる主要な化学反応式の概要を示しています。 Advance/FrontFlow/red の詳細反応モデルを用いることで、温度や流速分布だけでなく、 反応に寄与する各化学種の質量分率/モル分率分布、さらには、 使用した化学反応式ごとの反応速度なども可視化することが可能であり、 化学反応の詳細なメカニズムの考察が可能です。
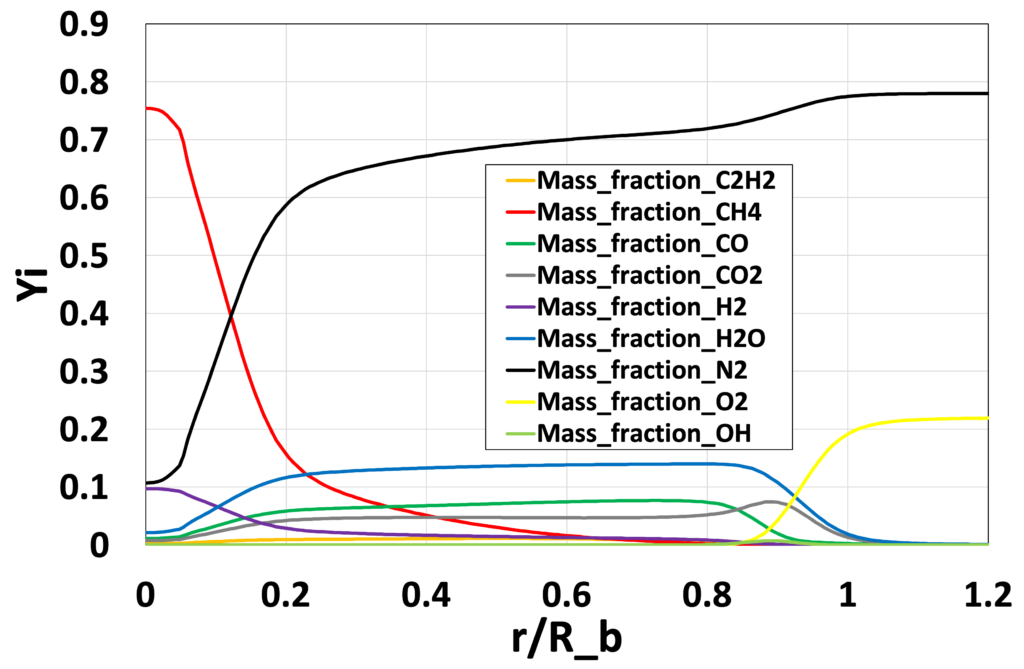
図16:半径方向の主要な化学種の質量分率\(\overline{Y_i}\)分布 (Medium grid without EDC, \(x/D_b=0.26\))
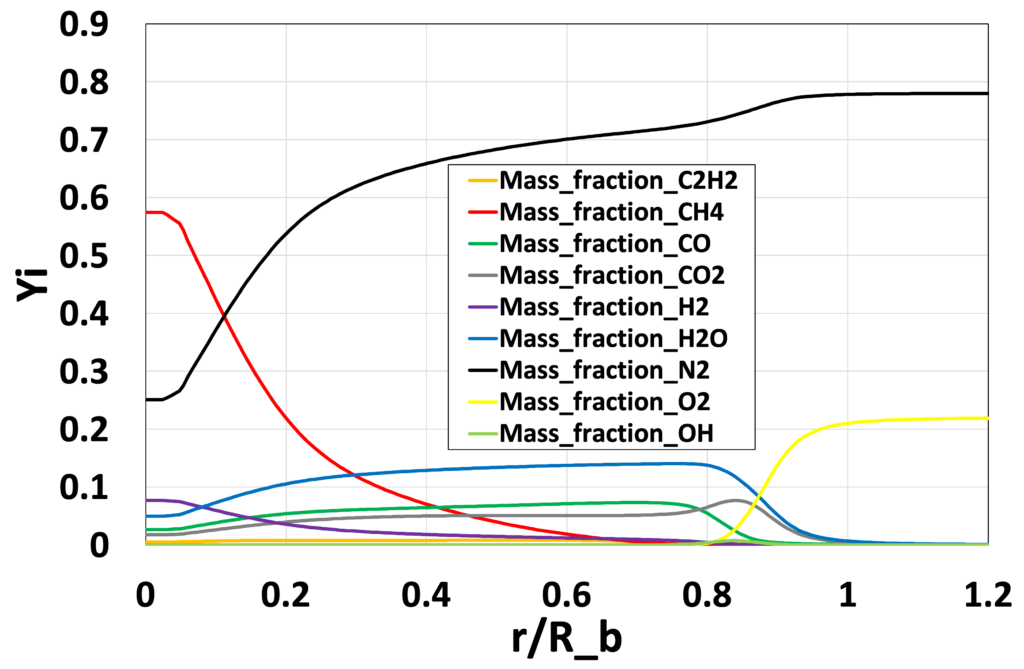
図17:半径方向の主要な化学種の質量分率\(\overline{Y_i}\)分布 (Medium grid without EDC, \(x/D_b=0.6\))
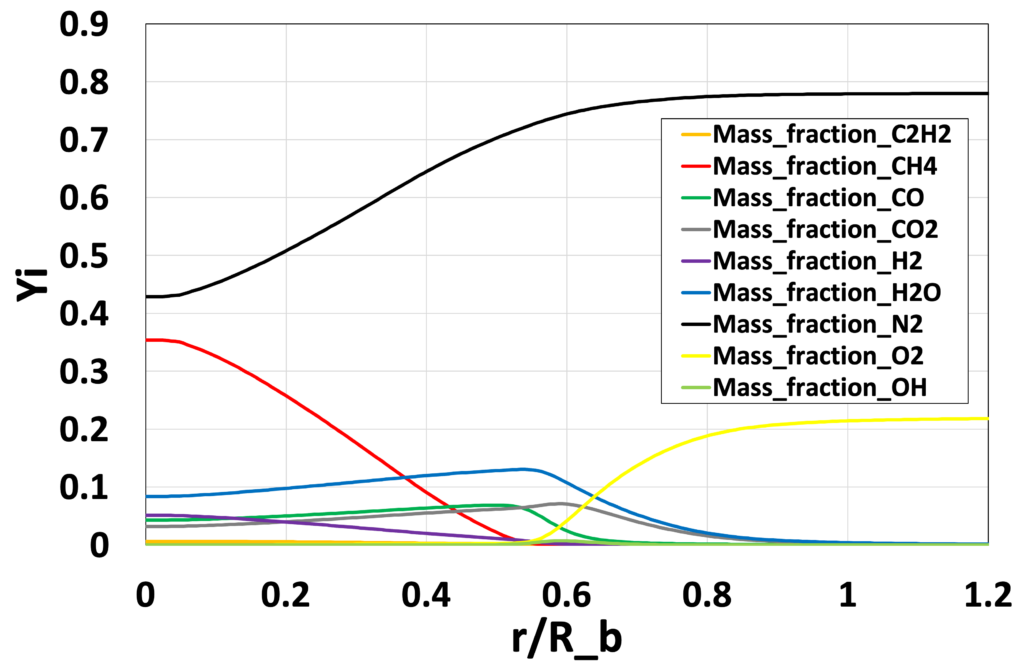
図18:半径方向の主要な化学種の質量分率\(\overline{Y_i}\)分布 (Medium grid without EDC, \(x/D_b=1.3\))
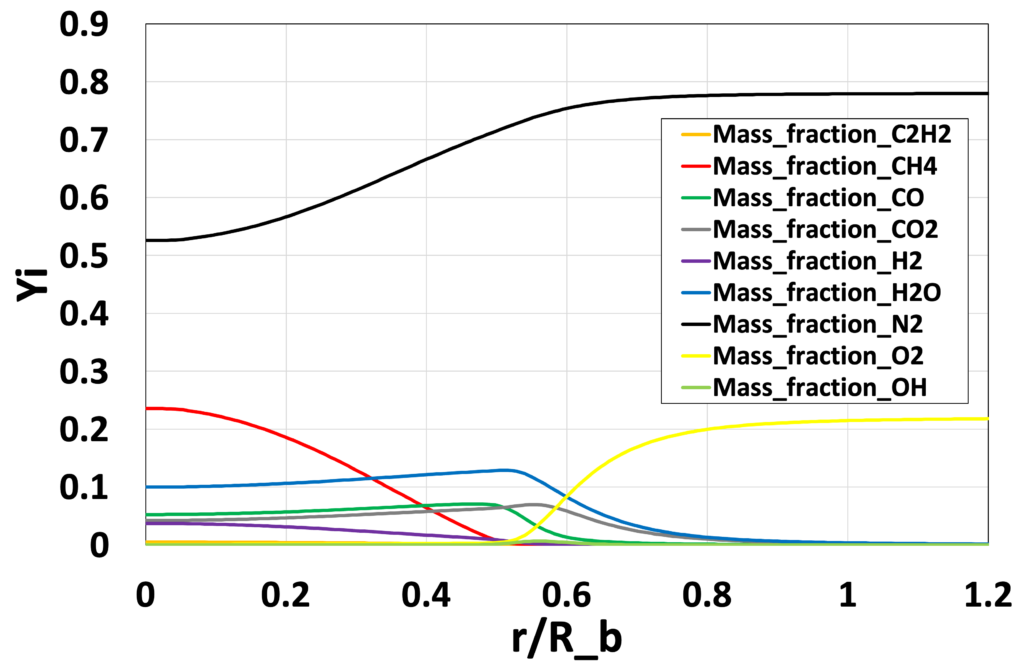
図19:半径方向の主要な化学種の質量分率\(\overline{Y_i}\)分布 (Medium grid without EDC, \(x/D_b=1.8\))
表2:OHの生成に関わる主要な化学反応式
| 化学反応メカニズム内における 化学反応式番号 | 左辺 | 右辺 | 反応速度の正負 |
| 3 | ‘H2′,’O’ | ‘H’,’OH’ | 正 |
| 38 | ‘H’,’O2′ | ‘O’,’OH’ | 正 |
| 84 | ‘H2′,’OH’ | ‘H’,’H2O’ | 正 |
| 86 | ‘OH’ | ‘H2O’,’O’ | 負 |
| 99 | ‘CO’,’OH’ | ‘CO2′,’H’ | 正 |
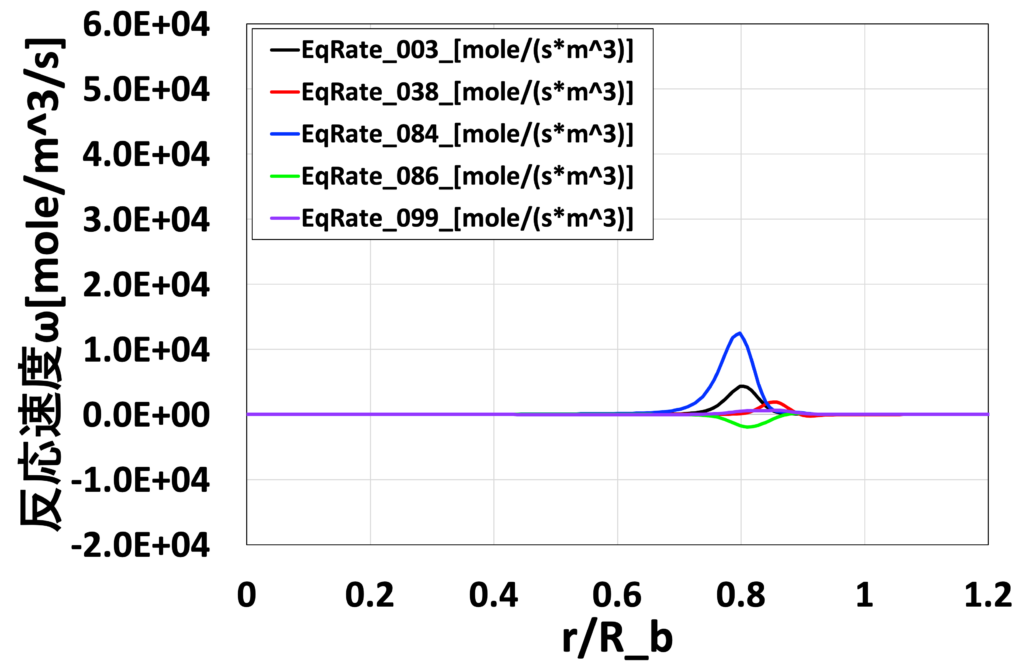
図20:半径方向の化学反応速度 \(\overline{\dot{\omega}_j} [mol/ \left( m^3 \cdot s \right)]\)分布 (Medium grid without EDC, \(x/D_b=0.26\))
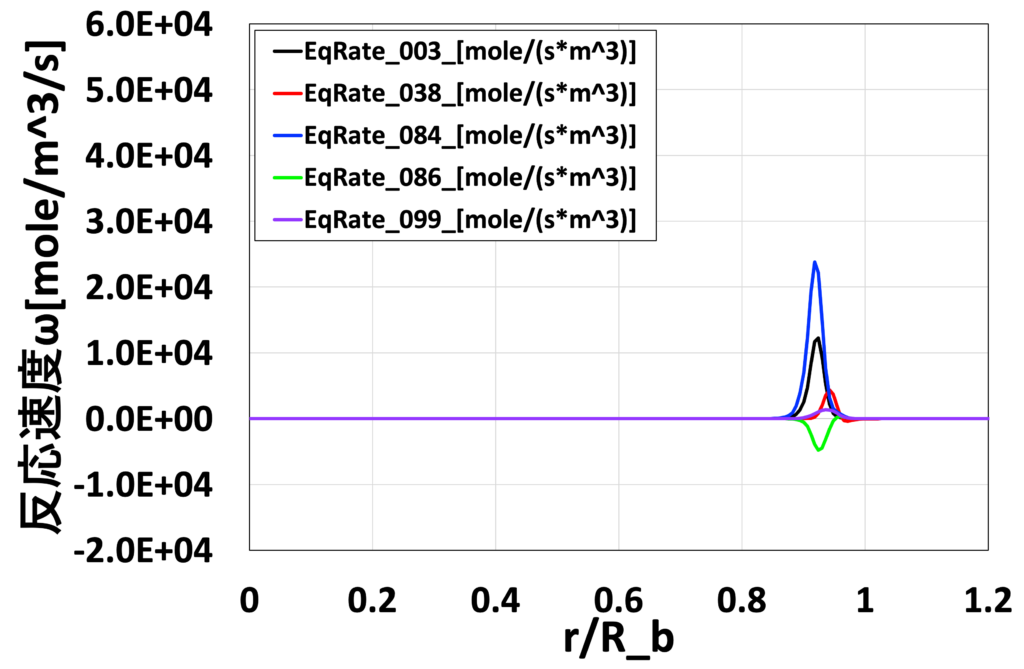
図21:半径方向の化学反応速度 \(\overline{\dot{\omega}_j} [mol/ \left( m^3 \cdot s \right)]\)分布 (Medium grid without EDC, \(x/D_b=0.26\))
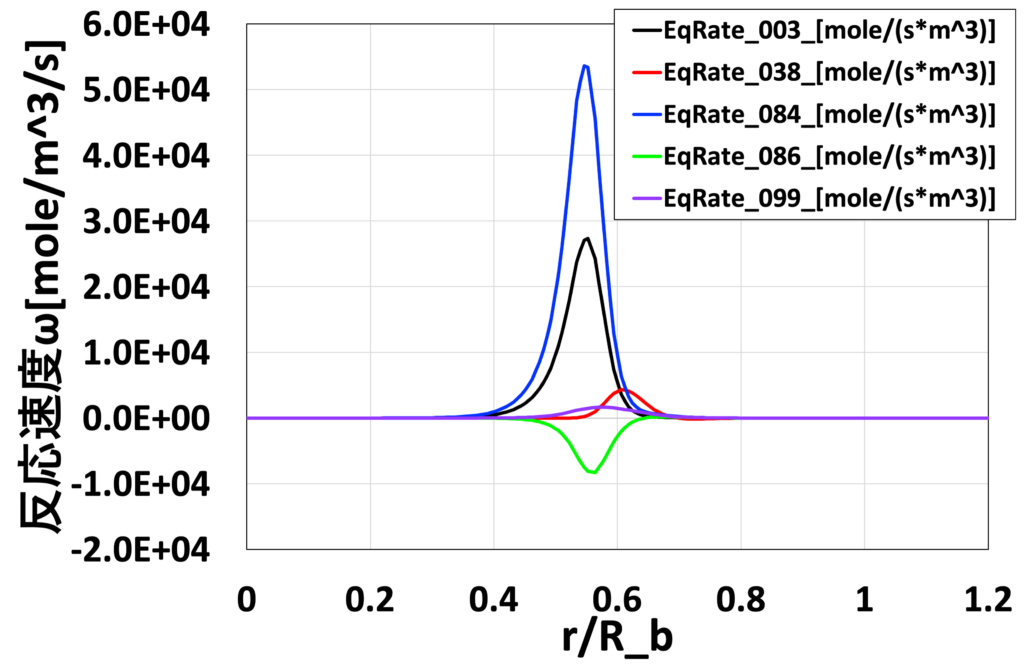
図22:半径方向の化学反応速度 \(\overline{\dot{\omega}_j} [mol/ \left( m^3 \cdot s \right)]\)分布 (Medium grid without EDC, \(x/D_b=1.3\))
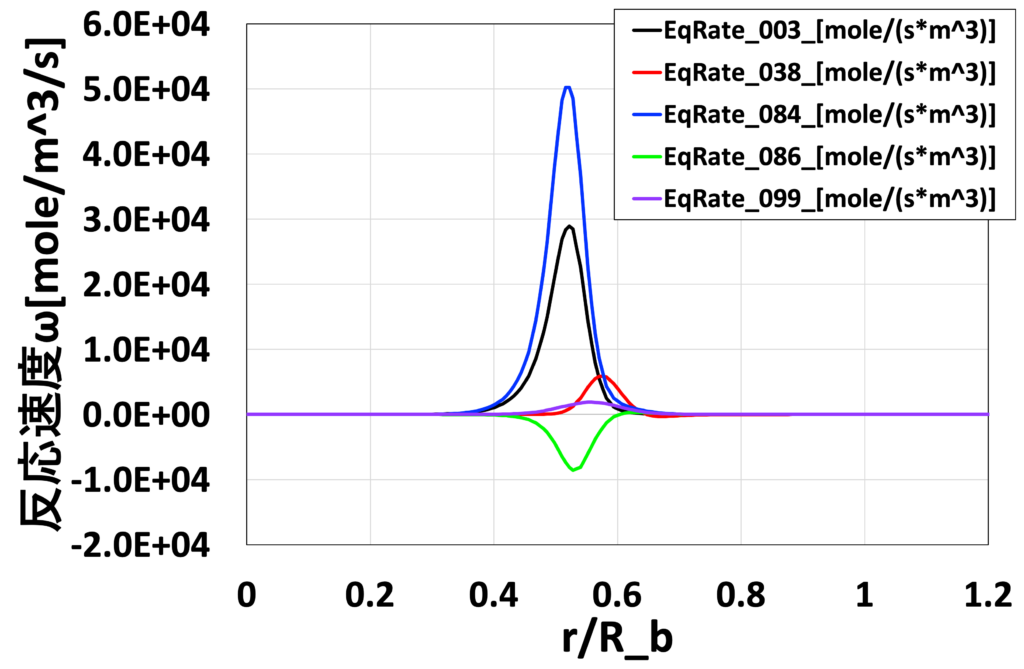
図23:半径方向の化学反応速度 \(\overline{\dot{\omega}_j} [mol/ \left( m^3 \cdot s \right)]\)分布 (Medium grid without EDC, \(x/D_b=1.8\))
参考文献
- “International Workshop on Measurement and Computation of Turbulent Flames (TNF Workshop),” https://tnfworkshop.org/data-archives/bluffbod/, (Accessed May, 2025).
- Ren, Z., Goldin, M. G., Hiremath, V., Pope, B. S., “Simulations of a turbulent non-premixed flame using combined dimension reduction and tabulation for combustion chemistry,” Fuel, Vol. 105, pp. 636–644, 2013.
- Smith, P. G., Golden, M. D., Frenklach, M., Moriarty, W. N., Eiteneer, B., Goldenberg, M., Bowman, T. C., Hanson, K. R., Song, S., Gardiner, C. W. Jr., Lissianski, V. V., & Qin, Z., “GRI-Mech 3.0,” http://www.me.berkeley.edu/gri_mech/, 2003 (Accessed May, 2025).
- Magnussen, B. F., “On the structure of turbulence and a generalized eddy dissipation concept for chemical reaction in turbulent flow,” Proceedings of the 19th Aerospace Sciences Meeting, AIAA paper 81-042, 1981.
- Barlow, R. S., “Sandia H2/He Flame Data – Release 2.0,” https://tnfworkshop.org/data-archives/simplejet/h2he/, Sandia National Laboratories, 2003 (Accessed May, 2025).

